blue physics

"Ick hab nen Pfeil aufn Kopp, ick bin nen Vektor!"

komischerweise kommt man auf EU-Einigungsvertäge, wenn man das bei Wikipedia eingibt... Wer den ganzen Kram in Formelform haben will schaut auf: http://www.math.uni-magdeburg.de/lehrver/analysis1_WS_04_05/reihen_4.pdf

Was ist eine Reihe? Dämliche Frage oder? Der nichteingeweite kennt eine Reihe Bücher, eine Reihe Lippenstifte im Schminkregal, eine Reihe von Soldaten die beim Apell stehen.
Was haben diese Reihen alles gemeinsam? Na dass sie nach einer bestimmten Ordnung aufgestellt sind. Nun, diese Art des Hintereinanderaufstellens ist mathematisch gesehen keine Reihe sondern eine Folge. Sorry aber mit diesem Unsinn muss man sich nunmal abfinden: Nach Autor sortierte Bücher, nach Größe sortierte Kinder, nach Farbe Form und Größe sortierte Schuhe (kann also auch schwieriger sein unser Ordnungssystem), sind, wenn man sie brav durch Kommas trennt eine Folge und die Kinder, Bücher, Schuhe usw. sind Glieder der Folge.

Ja aber was ist denn nun eine Reihe?

Nun als erstes braucht man eine Regel, wie man Glieder einer Folge zusammenzählen kann. Hat man eine Folge von Zahlen so nennt man dieses Zusammenzählen meistens "+" oder "plus rechnen" aber auch "summieren". Man kann auch Schuhe und Kinder zusammenrechnen, wenn man dafür geeignete Regeln aufstellt.
Eine Reihe ist nun nichts anderes als alle meine Folgenglieder zusammengerechnet, also die Summe aller Glieder einer Folge.

Häääääh? Konvergenz???

Naja das ist so... Wenn meine Folge nicht unendlich lang ist kann ich ja ausrechnen wie groß meine Reihe ist, indem ich alle Folgenglieder zusammenrechne. Aber wenn in meiner Folge nunmal verdammt viele Glieder stehen, kann das in eine Heidenarbeit ausarten. Und wenn unendlich viele Folgenglieder da sind brauch ich gar nicht erst anzufangen, da werd ich eh nicht fertig. Wenn ich nun aber wissen möchte, welchen Wert meine Reihe hat, oder (falls sie unendlich ist) ob sie überhaupt einen hat (ob sie "KONVERGIERT"), dann kann man sich die Art und Weise, wie die Glieder der Folge sortiert sind ansehen und mit etwas Glück weiß man dann Bescheid, wenn man die Konvergenzkriterien kennt.

##Fangen wir mal mit dem Cauchy-Kriterium an und machen das Step by Step:

1. Ich denke mir eine höllisch absolut verdammt kleine, Zahl größer als null aus und nenne diese Epsilon.

2. Ich lege mein Augenmerk auf die Folge in meiner Reihe.

3. Ich suche zwei hintereinanderstehende Glieder meiner Folge raus.
-Ich zähle die beiden zusammen.
-Falls da was negatives rauskommt, mache ich
das minus weg.

4. Falls ich zwei Folgenglieder finden kann, die kleiner als jedes beliebige Epsilon sind konvergiert die Folge.


##Man kann auch sagen, dass die Folge in einer konvergenten Reihe eine Nullfolge ist, also die Glieder immer immer kleiner werden bis sie irgendwann (vielleicht im undenlichen) null sind. Achtung nur weil eine Nullfolge in einer Reihe steckt, konvergiert diese nicht unbedingt.


Falls man übigens feststellt, das die Reihe nur konvergiert, falls man die negativen Vorzeichen der Folgeglieder unter den Tisch fallen lässt, so nennt man die Reihe "absolut konvergent".

##Jede absolut konvergente Reihe ist konvergent.

Betrachten wir von nun an nur Reihen mit positiven Gliedern...

## Schneide ich meine unendliche Reihe an einer beliebigen Stelle ab und ich finde raus, das diese dann eine obere Grenze hat (sie ist beschränkt), dann ist sie uch konvergent. Und: Wenn eine Reihe konvergent ist kann ich sie irgendwo abschneiden und werde garantiert eine obere Schranke für sie finden.

## Das Quotientenkriterium

Wenn ich irgendwann weit hinten in meiner Folge eine Folgenglied durch seinen Vorgänger teile und das ist kleiner 1, dann konvergiert die Folge.

## Das Majorantenkritrium

Eine Majorante der Reihe 1, ist eine Reihe2 deren Glieder ab einen bestimmten Punkt immer größer sind als die Glieder der Reihe 1.

Wenn nun die Majorante konvergiert, muss auch die Reihe selbst konvergieren, denn sie wird ja von der Majorante zusammengequetscht.

Heute hab ich viel Zeit mit meinen Mathe-Hausaufgaben verbracht. Das Ergebnis ist, dass ich jetzt eine ungefähre Ahnng vom Satz von Stokes und vom Satz von Gauß habe, Green hingegen, dieser kleine Kokser, der wird mir wohl immer verschlossen bleiben.

Also nun zu Stokes:

Wenn man berechnen will wie doll das Wasser in einem Wirpool strudelt, dann kann ich mir jeden einzelnen Strudel anschauen und die Wirkung von denen zusammenzählen oder ich schaue mir einfach an, wie das Wasser am Rand des Pools herumfließt.



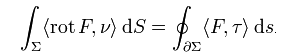
Gauß hatte ähnliche Probleme:

Nehmen wir an wir hätten einen löcherigen Sack voll Wasser und aufgedrehter Wasserhähne. Der kluge Gauß hat nun herausgefunden, dass genauso viel Wasser aus der Oberfläche des Sacks herauskommt, wie Wasser aus den Hähnen in den Sack hineinfließt. Natürlich ist der Sack nicht dehnbahr und das Wasser sei nicht kompressibel.




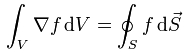
Wow, wenn man das so ausdrückt ist es gar nicht so schwer. Als Formel sieht das oll aus. Vielen Dank an David J. Griffiths für diese tollen anschaulichen Erklärungen.

Außerdem habe ich in der Übung zur theoretischen Elektrodynamik gelernt, dass man mit Hilfe dieser Erkenntnis die Maxwellschen Gleichungen umformen kann. Außerdem kann man ganz leicht aus den Maxwell- Sachen die Kontinuitätsgleichung herleiten. Klingt abgehoben, aber das Ding sagt nur aus das in einem Sack Kartoffeln immer gleich viele Kartoffeln bleiben, plus die die ich dazutue, minus die ich wegnehme.



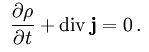
Man sieht also wir beschäftigen uns mit Themen, die die Menschheit bewegen und schaffen es die einfachsten Sachverhalte in die bescheuertesten Formeln zu verpacken.