blue physics

Heute hab ich viel Zeit mit meinen Mathe-Hausaufgaben verbracht. Das Ergebnis ist, dass ich jetzt eine ungefähre Ahnng vom Satz von Stokes und vom Satz von Gauß habe, Green hingegen, dieser kleine Kokser, der wird mir wohl immer verschlossen bleiben.

Also nun zu Stokes:

Wenn man berechnen will wie doll das Wasser in einem Wirpool strudelt, dann kann ich mir jeden einzelnen Strudel anschauen und die Wirkung von denen zusammenzählen oder ich schaue mir einfach an, wie das Wasser am Rand des Pools herumfließt.



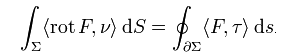
Gauß hatte ähnliche Probleme:

Nehmen wir an wir hätten einen löcherigen Sack voll Wasser und aufgedrehter Wasserhähne. Der kluge Gauß hat nun herausgefunden, dass genauso viel Wasser aus der Oberfläche des Sacks herauskommt, wie Wasser aus den Hähnen in den Sack hineinfließt. Natürlich ist der Sack nicht dehnbahr und das Wasser sei nicht kompressibel.




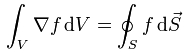
Wow, wenn man das so ausdrückt ist es gar nicht so schwer. Als Formel sieht das oll aus. Vielen Dank an David J. Griffiths für diese tollen anschaulichen Erklärungen.

Außerdem habe ich in der Übung zur theoretischen Elektrodynamik gelernt, dass man mit Hilfe dieser Erkenntnis die Maxwellschen Gleichungen umformen kann. Außerdem kann man ganz leicht aus den Maxwell- Sachen die Kontinuitätsgleichung herleiten. Klingt abgehoben, aber das Ding sagt nur aus das in einem Sack Kartoffeln immer gleich viele Kartoffeln bleiben, plus die die ich dazutue, minus die ich wegnehme.



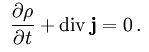
Man sieht also wir beschäftigen uns mit Themen, die die Menschheit bewegen und schaffen es die einfachsten Sachverhalte in die bescheuertesten Formeln zu verpacken.